Numpy
约 6216 字大约 21 分钟
2025-10-03
Numpy是Python中进行科学计算的基础包。它提供了一个强大的N维数组对象ndarray,以及用于操作这些数组的各种函数和工具。
基本数组类-ndarray
Numpy的基本数组类被称为 ndarray, 它表示一个“N 维数组”, ndarray具有以下特点:
ndarray的所有元素必须具有相同的数据类型。如果创建ndarray时列表包含不同数据类型,NumPy会自动转换为统一数据类型,优先级:
str > float > int。ndarray的大小在创建后不能更改。
此外, ndarray 还具有以下属性:
ndarray.shape- 返回数组的形状, 以元组形式表示每个维度的大小ndarray.size- 返回数组中固定总元素数, 等于ndarray.shape元素的乘ndarray.dtype- 返回数组元素的数据类型ndarray.itemsize- 返回数组中每个元素的字节大小ndarray.ndim- 返回数组维度
广播机制
广播(Broadcast)是 numpy 对不同形状(shape)的数组进行数值计算的方式。它允许在不同形状的数组之间进行算术运算,而不需要显式地调整它们的形状。
ndarray广播机制的规则:
- 为缺失的维度补维度
- 确实元素用已有值补充
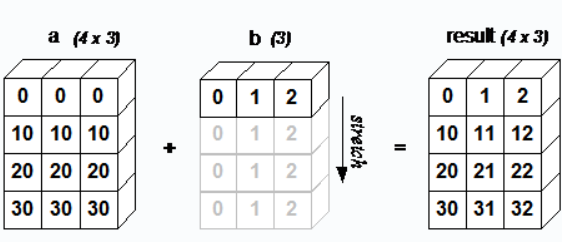
示例:
a = np.array([[ 0, 0, 0],
[10,10,10],
[20,20,20],
[30,30,30]])
b = np.array([0,1,2])
print(a + b)
# 输出结果
# [[ 0 1 2]
# [10 11 12]
# [20 21 22]
# [30 31 32]]数组b通过补充维度和补充已有值来实现其形状与a相同
打印
Numpy打印ndarray遵循以下规则:
- x轴从左到右打印,代表有多少列
- y轴从前到后打印,代表有多少行
- z轴从上到下打印,代表有多少个矩阵
一维数组打印为行,二维数组打印为矩阵,三维数组打印为矩阵列表:
import numpy as np
# 一维数组打印为行
a = np.array([1,2,3])
print(a)
[1 2 3]
# 二维数组打印为矩阵
b = np.array([[1,2,3],[4,5,6]])
print(b)
[[1 2 3]
[4 5 6]]
# 三位数组打印为矩阵列表
c = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
print(c)
[[[ 1 2 3]
[ 4 5 6]]
[[ 7 8 9]
[10 11 12]]]如果数组太大而无法打印,NumPy 会自动跳过数组的中间部分,只打印角落部分:
import numpy as np
a = np.arange(10000).reshape(10, 10)
print(a)
# [[ 0 1 2 3 4 5 6 7 8 9]
# [ 10 11 12 13 14 15 16 17 18 19]
# [ 20 21 22 23 24 25 26 27 28 29]
# ...
# [ 70 71 72 73 74 75 76 77 78 79]
# [ 80 81 82 83 84 85 86 87 88 89]
# [ 90 91 92 93 94 95 96 97 98 99]]要禁用此行为并强制 NumPy 打印整个数组,可以使用 set_printoptions 更改打印选项:
import numpy as np
np.set_printoptions(threshold=sys.maxsize) # 设置打印选项,强制打印整个数组
print(a)
# [[ 0 1 2 3 4 5 6 7 8 9]
# [ 10 11 12 13 14 15 16 17 18 19]
# [ 20 21 22 23 24 25 26 27 28 29]
# [ 30 31 32 33 34 35 36 37 38 39]
# [ 40 41 42 43 44 45 46 47 48 49]
# [ 50 51 52 53 54 55 56 57 58 59]
# [ 60 61 62 63 64 65 66 67 68 69]
# [ 70 71 72 73 74 75 76 77 78 79]
# [ 80 81 82 83 84 85 86 87 88 89]
# [ 90 91 92 93 94 95 96 97 98 99]]创建ndarray
关联np.array()、np.zeros()、np.ones()、np.empty()、np.arange()、np.linspace()等函数。
np.array(object, dtype=None)
满足指定要求的数组对象。
>>> import numpy as np
>>> a = np.array([1, 2, 3], dtype=int)
>>> print(a)
[1 2 3]np.zeros(shape, dtype=float)
返回具有给定形状、数据类型的全0数组
>>> b = np.zeros(shape=(2, 2))
array([[ 0., 0.],
[ 0., 0.]])np.ones(shape, dtype=float)
返回一个指定形状和类型的全1数组。
>>> c = np.ones(shape=(2, 2), dtype=float)
array([[1., 1.],
[1., 1.]])np.empty(shape, dtype=float)
返回一个指定形状的未初始化数组。
>>> d = np.empty(shape=(2, 2), dtype=int)
array([[-1073741821, -1067949133],
[ 496041986, 19249760]])np.arange([start, ]stop, [step, ]dtype=None)
用于创建一个指定范围的数组。需要指定起始数字、结束数字和步长。
>>> e = np.arange(0, 10, 2)
>>> print(e)
[0 2 4 6 8]np.linspace(start, stop, num=50, endpoint=True, dtype=None, axis=0)
用于创建一个指定范围内的等间隔数组(等差数列)。
重要参数:
endpoint: 如果为True,stop将被包含在样本中,否则,它不包括在内。
>>> f = np.linspace(0, 1, 5)
>>> print(f)
[0. 0.25 0.5 0.75 1. ]随机数序列
关联random.randint()、random.randn()、np.random.normal()、random.random()等函数。
np.random.randint(low, high, size=None, dtype=None)
创建一个随机整数多维数组
np.random.randint(low, high, size, dtype)
# 参数说明:
# low:最小值
# high:最大值
# high=None时,数值范围为[0,low)区间内
# high非None时,数值范围在[low, high)区间内
# size=None:元组类型,表示数组的形状,默认只输出一个随机值
# dtype:元素类型# 生成一个2行3列,每个元素都在[3, 10)中取值的二维数组
>>> n = np.random.randint(low=3, high=10, size=(2, 3))
array([[6, 3, 7],
[5, 4, 8]])np.random.randn(d0, d1, ..., dn)
创造一个服从标准正态分布的多维数组
标准正态分布,又称为
u分布,是以0为均数、以1为标准差的正态分布,记为N(0, 1)
np.random.randn(d0, d1, ..., dn)
# 参数说明:
# dn:第n个维度的数值# 创建一个2行4列且元素值都符合标准正态分布的数组
>>> n = np.random.randn(2,4)
>>> n
array([[-0.6776552 , -0.61148814, -0.58947312, 0.69818486],
[-0.44196956, -0.58813179, -1.68624668, 0.51599455]])np.random.normal(loc=0.0, scale=1.0, size=None)
创建一个服从正态分布的多维数组
np.random.normal(loc=0.0, scale=1.0, size=None)
# 参数说明:
# loc:均值,对应着正态分布的中心
# scale:标准差,对应着分布的宽度,标准差越大,曲线越矮胖,反之越高瘦
# size:元组类型,对应着返回值数组的shape>>> n = np.random.normal(loc=100,scale=10,size=(3, 4))
>>> n
array([[100.53498161, 99.49691798, 98.56524008, 92.08966332],
[ 98.94132089, 113.85199291, 77.67732157, 91.31490689],
[ 97.06380556, 103.48698293, 100.15185344, 99.01669892]])np.random.random(size=None, dtype=np.float64)
创建一个值在[0,1)之间的多维数组
>>> n = np.random.random(size=(3,4))
>>> n
array([[0.20914518, 0.1956151 , 0.08665226, 0.46756406],
[0.35799504, 0.97141985, 0.54482715, 0.87104364],
[0.8695895 , 0.20469914, 0.45708104, 0.60093901]])添加元素
包含np.concatenate()、np.stack()、np.hstack()、np.vstack()、np.dstack()
np.concatenate((a1, a2, ...), axis=0, dtype=None)
沿着现有轴连接一系列数组。返回连接后的新数组。
>>> a = np.array([[1, 2], [3, 4]])
>>> b = np.array([[5, 6]])
>>> np.concatenate((a, b), axis=0) # 按列连接
array([[1, 2],
[3, 4],
[5, 6]])
>>> np.concatenate((a, b.T), axis=1) # 按行连接
array([[1, 2, 5],
[3, 4, 6]])
>>> np.concatenate((a, b), axis=None)
array([1, 2, 3, 4, 5, 6])np.stack(arrays, axis=0, dtype=None)
沿新轴连接一系列数组。
>>> a = np.array([[1, 2],
[3, 4]])
>>> b = np.array([[5, 6]])
>>> np.stack((a, b), axis=0) # 按列堆叠
array([[[1, 2]],
[[3, 4]],
[[5, 6]]])
>>> np.stack((a, b), axis=1) # 按行堆叠
array([[[1, 2],[5, 6]],
[[3, 4],[5, 6]]])np.hstack(n1,n2)
水平级联(左右合并)
>>> a = np.array([1, 2, 3])
>>> b = np.array([4, 5, 6])
>>> c = np.hstack((a, b))
>>> c
array([1, 2, 3, 4, 5, 6])np.vstack(n1,n2)
垂直级联(上下合并)
>>> a = np.array([1, 2, 3])
>>> b = np.array([4, 5, 6])
>>> c = np.vstack((a, b))
>>> c
array([[1, 2, 3],
[4, 5, 6]])np.dstack(n1,n2)
深度级联
>>> a = np.array([1, 2, 3])
>>> b = np.array([4, 5, 6])
>>> c = np.dstack((a, b))
>>> c
array([[[1, 4],
[2, 5],
[3, 6]]])删除元素
关联np.delete()、np.isin()、np.isnan()
np.delete(arr, obj, axis=None)
删除数组中的元素。
>>> a = np.array([[1, 2],
[3, 4]])
>>> np.delete(a, 0, axis=0) # 删除第一行
array([[3, 4]])
>>> np.delete(a, 1, axis=1) # 删除第二列
array([[1],
[3]])np.isin()
通过bool判断来过滤元素
>>> a = np.array([1, 2, 3, 4, 5])
>>> new_arr = a[a != 3] # 删除值为 3 的元素
>>> new_arr
array([1, 2, 4, 5])np.isnan()
使用布尔判断删除缺失值(NaN)
>>> arr = np.array([1, np.nan, 3, np.nan, 5])
>>> new_arr = arr[~np.isnan(arr)] # 使用 ~ 取反
>>> print(new_arr)
[1. 3. 5.]np.unique()
用于删除重复元素
>>> a = np.array([1, 2, 2, 3, 4, 4, 5])
>>> np.unique(a)
array([1, 2, 3, 4, 5])使用切片
适用于删除开头、结尾或连续的元素。
arr = np.array([1, 2, 3, 4, 5])
# 删除前两个元素
new_arr = arr[2:]
print(new_arr) # 输出: [3 4 5]查找元素
关联np.searchsorted()、np.where()、np.isin()、np.nonzero()、np.argmax()、np.argmin()等函数。
基于条件查找
np.where()
根据条件返回满足条件的元素的索引。
>>> a = np.array([1, 2, 3, 4, 5])
>>> np.where(a > 3)
(array([3, 4]),)np.isin()
判断元素是否在给定的数组中。
>>> a = np.array([1, 2, 3, 4, 5])
>>> a[np.isin(a, [2, 4])]
array([2, 4])np.all()
判断数组中所有元素是否都满足给定条件。
>>> a = np.array([1, 2, 3, 4, 5])
>>> np.all(a > 0)
True
>>> np.all(a < 4)
Falsenp.any()
判断数组中是否存在满足给定条件的元素。
>>> a = np.array([1, 2, 3, 4, 5])
>>> np.any(a > 4)
True
>>> np.any(a < 0)
False极值查找
np.argmax()
返回数组中最大值的索引。
>>> a = np.array([1, 2, 3, 4, 5])
>>> np.argmax(a)
4np.argmin()
返回数组中最小值的索引。
>>> a = np.array([1, 2, 3, 4, 5])
>>> np.argmin(a)
0非零元素查找
np.nonzero()
返回数组中非零元素的索引。
>>> a = np.array([1, 0, 2, 0, 3])
>>> np.nonzero(a)
(array([0, 2, 4]),)排序相关查找
np.searchsorted()
返回在已排序数组中插入元素的位置。
>>> a = np.array([1, 2, 3, 4, 5])
>>> np.searchsorted(a, 3)
2字符串数组查找
np.char.find()
返回子字符串在字符串数组中的起始位置。
>>> a = np.array(['hello', 'world', 'numpy'])
>>> np.char.find(a, 'o') # 查找子字符串 'o' 的起始位置
array([ 4, 1, -1])
>>> np.char.find(arr, 'o') >= 0 # 查找包含'o'的字符串
array([ True, True, False])元素排序
包含np.sort()、np.argsort()、np.lexsort()
np.sort()
默认返回升序排序后的新数组。
使用np.sort()对数组排序时可以指定轴、种类和顺序
函数说明
numpy.sort(a, axis=-1, kind=None, order=None, *, stable=None)
# 参数列表:
# a: array_like, 要排序的数组
# axis: int或None , 可选, 指定排序的轴,默认值为-1,表示沿最后一个轴排序
# kind: str,指定排序算法,默认值为'quicksort',可选值有:
# 'quicksort' - 快速排序
# 'mergesort' - 归并排序
# 'heapsort' - 堆排序
# 'stable' - 稳定排序
# order: str或str元组,可选,指定排序的字段名,适用于结构化数组
# stable: bool,可选,指定是否使用稳定排序,默认值为None,可选值有:
# True - 返回的数组将保持 a 中相等值的相对顺序
# False - 返回的数组不保持 a 中相等值的相对顺序
# 返回值:
# 返回排序后的新数组(与原数组各自独立,互不影响)。示例1: 初始数组
>>> a = np.array([[1,4],[3,1]])>>> np.sort(a) array([[1, 4], [1, 3]]) >>> np.sort(a, axis=0) # 沿着第0轴(列)排序 array([[1, 1], [3, 4]]) >>> np.sort(a, axis=1) # 沿着第1轴(行)排序 array([[1, 4], [1, 3]]) >>> np.sort(a, axis=None) # 数组扁平化(排序后变为一维数组) array([1, 1, 3, 4])示例2:
使用 order 关键字指定在对结构化数组排序时要使用的字段
初始数据
>>> dtype = [('name', 'S10'), ('height', float), ('age', int)] >>> values = [('Arthur', 1.8, 41), ('Lancelot', 1.9, 38), ('Galahad', 1.7, 38)] >>> a = np.array(values, dtype=dtype) # 创建结构化数组 >>> a array([('Arthur', 1.8, 41), ('Lancelot', 1.9, 38), ('Galahad', 1.7, 38)], dtype=[('name', '|S10'), ('height', '<f8'), ('age', '<i4')])按
height排序>>> np.sort(a, order='height') array([('Galahad', 1.7, 38), ('Arthur', 1.8, 41), ('Lancelot', 1.8999999999999999, 38)], dtype=[('name', '|S10'), ('height', '<f8'), ('age', '<i4')])按
age排序,如果年龄相同按height排序>>> np.sort(a, order=['age', 'height']) array([('Galahad', 1.7, 38), ('Lancelot', 1.8999999999999999, 38), ('Arthur', 1.8, 41)], dtype=[('name', '|S10'), ('height', '<f8'), ('age', '<i4')])
np.argsort()
返回数组元素排序后的索引数组
函数说明
numpy.sort(a, axis=-1, kind=None, order=None, *, stable=None)
# 参数列表:
# a: array_like, 要排序的数组
# axis: int或None , 可选, 指定排序的轴,默认值-1,表示沿最后一个轴排序, 如果为None, 则将数组展平为一维
# kind: str,指定排序算法,默认值为'quicksort',可选值有:
# 'quicksort' - 快速排序
# 'mergesort' - 归并排序
# 'heapsort' - 堆排序
# 'stable' - 稳定排序
# order: str或str元组,可选,指定排序的字段名,适用于结构化数组
# stable: bool,可选,指定是否使用稳定排序,默认值为None,可选值有:
# True - 返回的数组将保持 a 中相等值的相对顺序
# False - 返回的数组不保持 a 中相等值的相对顺序
# 返回值:
# 返回排序后的新数组(与原数组各自独立,互不影响)。示例1: 二维数组
初始数组
>>> a = np.array([[3, 1, 4], [2, 5, 0]]) >>> a array([[3, 1, 4], [2, 5, 0]])>>> np.argsort(a) array([[1, 0, 2], [2, 0, 1]]) >>> np.argsort(a, axis=0) # 沿着第0轴(列)排序 array([[1, 0, 1], [0, 1, 0]]) >>> np.argsort(a, axis=1) # 沿着第1轴(行)排序 array([[0, 1, 2], [2, 0, 1]]) >>> np.argsort(a, axis=None) # 数组扁平化(排序后变为一维数组) array([0, 1, 1, 0])示例2: 带键排序
初始数组
>>> x = np.array([(1, 0), (0, 1)], dtype=[('x', '<i4'), ('y', '<i4')]) >>> x array([(1, 0), (0, 1)], dtype=[('x', '<i4'), ('y', '<i4')])先按
x排序,再按y排序>>> np.argsort(x, order=('x','y')) array([1, 0])先按
y排序,再按x排序>>> np.argsort(x, order=('y','x')) array([0, 1])
np.lexsort()
lexsort 返回一个整数索引数组,该数组描述了按多个键的排序顺序。
函数说明
numpy.lexsort(keys, axis=-1)
# 参数列表:
# keys: array_like, 用于排序的键数组,序列中的最后一个键用于主要排序顺序,其次是倒数第二个键用于打破平局,依此类推。
# axis: int或None, 可选, 指定排序的轴,默认值为-1,表示沿最后一个轴排序
# 返回值:
# 返回一个整形ndarray,该数组描述沿指定轴对键进行排序的索引数组。示例1:
初始数据
>>> a = [1, 5, 1, 4, 3, 4, 4] # First sequence >>> b = [9, 4, 0, 4, 0, 2, 1] # Second sequence根据两个数值键进行排序,首先按 a 的元素排序,然后按 b 的元素打破平局。
>>> ind = np.lexsort(keys=(b, a)) >>> ind array([2, 0, 4, 6, 5, 3, 1]) >>> [(a[i], b[i]) for i in ind] [(1, 0), (1, 9), (3, 0), (4, 1), (4, 2), (4, 4), (5, 4)]示例2:
重塑数组
重塑数组arr.reshape(new_shape)
使用array的reshape方法可以改变数组的形状,但不会改变数据本身。重塑后的数组与原数组共享数据,因此修改一个会影响另一个。
示例:
>>> a = np.array([0, 1, 2, 3, 4, 5]) >>> print(a) [0 1 2 3 4 5] >>> b = a.reshape((2, 3)) # 重塑为2行3列 >>> print(b) [[0 1 2] [3 4 5]]或者使用
np.reshape函数:>>> np.reshape(a, shape=(1, 6), order='C') array([[0, 1, 2, 3, 4, 5]]) # a: 原数组 # shape: 整数或整数元组,表示新形状 # order: 可选参数,指定元素的读取顺序, 默认值为'C' # 'C'表示按行读取, # 'F'表示按列读取, # 'A'表示按原数组的顺序读取
数组升维(添加新轴)
本节涵盖 np.newaxis、np.expand_dims
np.newaxis
使用np.newaxis可以在数组的任意位置添加一个新轴(维度),从而将一维变二维,二维变三维...
示例:
初始数组
>>> a = np.array([1, 2, 3, 4, 5, 6]) >>> a.shape (6,)使用
np.newaxis添加新轴>>> a2 = a[np.newaxis, :] >>> a2.shape (1, 6)np.newaxis还可以将一维数组转换为行向量或列向量# 沿第一个维度插入轴来将一维数组转换为行向量 >>> row_vector = a[np.newaxis, :] >>> row_vector.shape (1, 6) # 沿第二个维度插入轴将一维数组转换为列向量 >>> col_vector = a[:, np.newaxis] >>> col_vector.shape (6, 1)
np.expand_dims
使用 np.expand_dims 通过在指定位置插入新轴来扩展数组。
示例:
初始数组
>>> a = np.array([1, 2, 3, 4, 5, 6]) >>> a.shape (6,)使用
np.expand_dims在索引位置1处添加轴>>> b = np.expand_dims(a, axis=1) >>> b.shape (6, 1)在索引位置
0处添加轴>>> c = np.expand_dims(a, axis=1) >>> c.shape (1, 6)
索引和切片
索引
>>> n = np.random.randint(0, 10, size=(4,5))
>>> n
array([[6, 3, 1, 3, 2],
[4, 6, 6, 0, 8],
[7, 2, 8, 9, 3],
[5, 5, 9, 3, 3]])
# 输出最后一个元素
>>> n[-1][-1] # 可简写为n[-1, -1]
np.int64(3)
# 输出第二行第三列元素
>>> n[1][2] # 可简写为n[1, 2]
np.int64(6)切片
ndarray的切片操作与python列表完全一致,多维时同理
初始数组
# 多维数组
>>> n = np.array([[6, 3, 1, 3, 2],
[4, 6, 6, 0, 8],
[7, 2, 8, 9, 3],
[5, 5, 9, 3, 3]])行操作
取单行
>>> n[0]
array([6, 3, 1, 3, 2])取连续多行:切片
n[1:3]
>>> array([[4, 6, 6, 0, 8],
[7, 2, 8, 9, 3]])取不连续的多行:中括号
>>> n[[0,3]]
>>> array([[6, 3, 1, 3, 2],
[5, 5, 9, 3, 3]])行翻转
>>> n[::-1]
array([[5, 5, 9, 3, 3],
[7, 2, 8, 9, 3],
[4, 6, 6, 0, 8],
[6, 3, 1, 3, 2]])列操作
取一列
>>> n[:, 0] # 取所有行的第一个元素,即第一列
array([6, 4, 7, 5])
>>> n[0:2, 0] # 取前两行的第一个元素,即前两行的第一列
array([6, 4])取连续多列:切片
>>> n[:, 1:3] # 取第2和第3两列
array([[3, 1],
[6, 6],
[2, 8],
[5, 9]])
>>> n[0:2 , 1:3] # 取前两行的第2第3列
array([[3, 1],
[6, 6]])取不连续多列:中括号
>>> n[:,[0,2,4]] # 取第1列、第3列、第5列
array([[6, 1, 2],
[4, 6, 8],
[7, 8, 3],
[5, 9, 3]])
>>> n[0:2, [0,2,4]] # 取前两行的第1、2、5列
array([[6, 1, 2],
[4, 6, 8]])列翻转
>>> n[:, ::-1]
array([[2, 3, 1, 3, 6],
[8, 0, 6, 6, 4],
[3, 9, 8, 2, 7],
[3, 3, 9, 5, 5]])拆分
与级联类似,ndarray有三个函数完成拆分工作:
np.split()- 通用拆分,默认按行拆分
n = np.arange(9).reshape(3, 3)
n
# array([[0, 1, 2],
# [3, 4, 5],
# [6, 7, 8]])
n1 = np.split(n, 3, axis=0) # 按行平均拆分成3份
n1
# [array([[0, 1, 2]]),
# array([[3, 4, 5]]),
# array([[6, 7, 8]])]
n2 = np.split(n, [1, 2], axis=1) # 按列拆分,在第1列之后、第2列后分别切一刀,将整体分成3份
# [array([[0],
# [3],
# [6]]),
# array([[1],
# [4],
# [7]]),
# array([[2],
# [5],
# [8]])]np.vsplit()- 按行拆分
n = np.arange(16).reshape(4, 4)
# array([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11],
# [12, 13, 14, 15]])
n1 = np.vsplit(n, 2)
# [array([[0, 1, 2, 3],
# [4, 5, 6, 7]]),
# array([[ 8, 9, 10, 11],
# [12, 13, 14, 15]])]
n2 = np.vsplit(n, [1, 3]) # 在第1行后、第3行后分别切一刀,将整体分成3份
n2
# [array([[0, 1, 2, 3]]),
# array([[ 4, 5, 6, 7],
# [ 8, 9, 10, 11]]),
# array([[12, 13, 14, 15]])]np.hsplit()- 按列拆分
n = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
n1 = np.hsplit(n, 4) # 按列平均拆成4份
n1
# [array([[1],
# [5],
# [9]]),
# array([[2],
# [6],
# [10]]),
# array([[3],
# [7],
# [11]]),
# array([[4],
# [8],
# [12]])]
result = np.hsplit(arr, [2, 3]) # 在第2列和第3列后分别切一刀,整体分成3份
result
# [array([[1, 2],
# [5, 6],
# [9, 10]]),
# array([[3],
# [7],
# [11]]),
# array([[4],
# [8],
# [12]])]拷贝、浅拷贝与深拷贝
- 赋值拷贝 - 两者引用同一内存,A变B也变
n = np.arange(10)
n2 = n
n2[0] = 100
display(n, n2)
# array([100, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# array([100, 1, 2, 3, 4, 5, 6, 7, 8, 9])- copy() - 深拷贝
n = np.arange(10)
n2 = n.copy()
n2[0] = 100
display(n, n2)
# array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# array([100, 1, 2, 3, 4, 5, 6, 7, 8, 9])聚合操作
速查
np.sum(): 求和np.min(): 最小值np.max(): 最大值np.mean(): 平均值np.average(): 平均值np.medium(): 中位数np.percentile(): 百分位数np.argmin(): 最小值对应的下标np.argmax(): 最大值对应的下标np.std(): 标准差np.var(): 方差np.power(): 次方,求幂np.argwhere(): 按条件查找
示例代码
np.sum()
# 一维数组直接求和
n = np.arange(10)
n
# array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
s1 = np.sum(n)
s1
# np.int64(45)
# 多维数组求和
# axis=0: 按行求和
n = np.random.randint(0,10,size=(3,4))
# [[1 2 5 9]
# [2 6 8 3]
# [0 0 8 7]]
s2 = np.sum(n, axis=0) # 从上到下求和
s2
# array([3, 8, 21, 19])
# axis=1: 按列求和
s3 = np.sum(n, axis=1) # 从右往左求和
s3
# array([17, 19, 15])np.min()
# 一维数组最小值
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
m1 = np.min(n)
m1
# np.int64(0)np.max()
# 一维数组最大值
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
m2 = np.max(n)
m2
# np.int64(9)np.mean()
# 一维数组平均值
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
m3 = np.mean(n)
m3
# np.float64(4.5)np.average()
# 一维数组平均值
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
m4 = np.average(n)
m4
# np.float64(4.5)np.median()
# 一维数组中位数
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
m5 = np.median(n)
m5
# np.float64(4.5)np.percentile()
# 一维数组百分位数
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
p1 = np.percentile(n, 50) # 50%分位数
p1
# np.float64(4.5)
p2 = np.percentile(n, 75) # 75%分位数
p2
# np.float64(6.75)np.argmin()
# 一维数组最小值对应的下标
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
a1 = np.argmin(n)
a1
# np.int64(0) # 最小值0在第0个位置np.argmax()
# 一维数组最大值对应的下标
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
a2 = np.argmax(n)
a2
# np.int64(9) # 最大值9在第9个位置np.std()
# 一维数组标准差
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
s1 = np.std(n)
s1
# np.float64(2.8722813232690143) # 标准差np.var()
# 一维数组方差
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
v1 = np.var(n)
v1
# np.float64(8.25) # 方差np.power()
# 一维数组求幂
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
p1 = np.power(n, 2) # 求平方
p1
# array([ 0, 1, 4, 9, 16,
# 25, 36, 49, 64, 81]) # 每个元素平方np.argwhere()
# 一维数组按条件查找
n = np.arange(10)
n
# array([0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9])
a1 = np.argwhere(n > 5) # 查找大于5的元素
a1
# array([[6],
# [7],
# [8],
# [9]])其他常见聚合操作
np.unique()
查找数组中的唯一值
import numpy as np
# 创建一个包含重复元素的数组
arr = np.array([1, 2, 2, 3, 4, 4, 5])
# 查找唯一值
unique_values = np.unique(arr)
print(unique_values)
# 输出结果
# [1 2 3 4 5]数学常数与符号
Numpy提供了丰富的数学函数来进行数组的数学运算,包括基本的算术运算、三角函数、指数和对数等。
np.abs() # 绝对值
np.sqrt() # 平方根
np.square() # 平方
np.exp() # 指数, e=2.71828
np.log() # 自然对数, 以e为底
np.log10() # 以10为底的对数
np.sin() # 正弦
np.cos() # 余弦
np.tan() # 正切
np.arcsin() # 反正弦
np.arccos() # 反余弦
np.arctan() # 反正切
np.round() # 四舍五入
np.floor() # 向下取整
np.ceil() # 向上取整
np.mod() # 取模
np.remainder() # 取余数
np.gcd() # 最大公约数
np.lcm() # 最小公倍数
np.power() # 幂运算
np.radians() # 角度转弧度
np.degrees() # 弧度转角度矩阵运算
矩阵加减
import numpy as np
# 创建两个矩阵
a = np.array([[1, 2],
[3, 4]])
b = np.array([[5, 6],
[7, 8]])
c = a + b
c
# array([[ 6, 8],
# [10, 12]])
d = a - b
d
# array([[-4, -4],
# [-4, -4]])矩阵乘法
a = np.array([[1, 2],
[3, 4]])
b = np.array([[5, 6],
[7, 8]])
# 1.矩阵的数乘运算:矩阵*标量
c = 2 * a # 矩阵a的每个元素都乘以2
c
# array([[2, 4],
# [6, 8]])
# 2.矩阵的积:矩阵*矩阵
# 使用@符号或np.dot()函数
d = a @ b
d
# array([[19, 22],
# [43, 50]])
e = np.dot(a, b)
e
# array([[19, 22],
# [43, 50]])矩阵转置
import numpy as np
# 创建一个矩阵
a = np.array([[1, 2],
[3, 4]])
# 矩阵转置
b = a.T
b
# array([[1, 3],
# [2, 4]])矩阵的逆
矩阵的逆:满足A * A^-1 = E的矩阵A^-1称为矩阵A的逆矩阵,其中E为单位矩阵。
import numpy as np
# 创建一个矩阵
a = np.array([[1, 2],
[3, 4]])
# 矩阵的逆
b = np.linalg.inv(a)
b
# array([[-2. , 1. ],
# [ 1.5, -0.5]])
# 验证逆矩阵
c = np.dot(a, b)
c
# array([[1., 0.],
# [0., 1.]])矩阵的行列式
行列式计算:主对角线和 - 副对角线线和
import numpy as np
# 创建一个矩阵
a = np.array([[1, 2],
[3, 4]])
# 计算行列式
d = np.linalg.det(a)
d
# array(-2.0)
# 验证行列式
e = np.linalg.det(b)
e
# array(1.0)矩阵的秩
矩阵的秩:最大线性无关行(列)数
import numpy as np
# 创建一个矩阵
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# 计算矩阵的秩
r = np.linalg.matrix_rank(a)
r
# array(2) # 矩阵的秩为2文件操作
Numpy提供了简单的文件读写功能,可以将数组保存到磁盘或从磁盘加载数组。
保存数组到文件
np.save():将数组保存到二进制文件中,文件扩展名为.npy。
import numpy as np
# 创建一个数组
arr = np.array([[1, 2, 3], [4, 5, 6]])
# 保存数组到文件
np.save('array.npy', arr)
# 保存数组到文本文件
np.savetxt('array.txt', arr, fmt='%d') # fmt指定保存的格式np.savez():将多个数组保存到一个压缩文件中,文件扩展名为.npz。
import numpy as np
# 创建多个数组
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
# 保存多个数组到压缩文件
np.savez('arrays.npz', array1=arr1, array2=arr2)np.savetxt():保存到csv、txt文件
import numpy as np
# 创建一个数组
arr = np.array([[1, 2, 3], [4, 5, 6]])
# 保存数组到CSV文件
np.savetxt('array.csv', arr, delimiter=',', fmt='%d') # delimiter指定分隔符,fmt指定保存的格式
# 保存数组到文本文件
np.savetxt('array.txt', arr, fmt='%d') # fmt指定保存的格式从文件中读取
np.load():从.npy文件中加载数组。
import numpy as np
# 从.npy文件中加载数组
arr = np.load('array.npy')
print(arr)
# 输出结果
# [[1 2 3]
# [4 5 6]]np.loadtxt():从csv、txt文件中读取
import numpy as np
# 从CSV文件中加载数组
arr_csv = np.loadtxt('array.csv', delimiter=',', dtype=np.int16) # delimiter指定分隔符,dtype指定数据类型
print(arr_csv)
# 输出结果
# [[1 2 3]
# [4 5 6]]
# 从文本文件中加载数组
arr_txt = np.loadtxt('array.txt', dtype=int) # dtype指定数据类型
print(arr_txt)
# 输出结果
# [[1 2 3]
# [4 5 6]]